Inhaltsverzeichnis
Parallelisieren
The Free Lunch is over.— Herb Sutter
Über Jahrzehnte haben Programmierer die Laufzeit-Effizienz von Programmen vernachlässigt. Emulatoren, virtuelle Maschinen, interpretierende Systeme konnten von schnelleren Prozessoren mit immer mehr Speicher profitieren. Doch schon dabei hatte (nicht nur) ich den Eindruck, dass die Hardware langsamer beschleunigt als die Software langsamer wird. Die Taktraten wachsen nicht mehr, wie Sutters Artikel vom März 2005 zeigt. Allenfalls die Zahl der Rechenkerne pro Maschine steigt noch ein paar Jahre.
Ein Zuwachs an Leistungsfähigkeit ist nicht mehr kostenlos zu haben. Parallele_Programmierung verteilt die Datenverarbeitung auf mehrere Rechenkerne, Prozessoren bzw. Maschinen. Dazu müssen die Programmquellen verändert werden. Prozessoren und Compiler können nur begrenzt erkennen, welche Teile eines Programms für nebenläufige Abarbeitung geeignet sind. Zur Wahl geeigneter Algorithmen, Datenstrukturen und Kommunikationsstrategien kommen noch ein paar alte, fast in Vergessenheit geratene Tugenden: Programmierdisziplin, Messen und gezieltes Optimieren. Nebenbei spielt auch die Wahl der Programmiersprache eine Rolle. Hier werden Ansätze in C++ untersucht.
Amdahls Gesetz
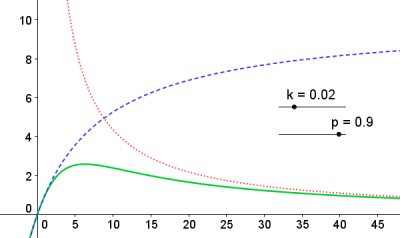
Die Geschwindigkeitssteigerung (engl. speedup) S eines parallelisierbaren Programms hängt von der Anzahl n verfügbarer Prozessoren bzw. Kerne ab: \[ S(n) = \frac{t_{\rm sequentiell}}{t_{\rm parallelisiert}} = \frac{1}{1-p + \frac{p}{n}} < \frac{1}{1-p}. \] Darin ist 0 ≤ p ≤ 1 der Anteil parallelisierter Schritte. In Amdahls Gesetz (blaue Kurve) wird der Kommunikationsaufwand k(n) ~ O(n) (rote Kurve) zwischen parallelen und seriellen Abschnitten nicht berücksichtigt. In der modifizierten Form (grüne Kurve) \[ S(n) = \frac{1}{1-p + k \cdot n + \frac{p}{n}} \] existiert ein ausgeprägtes Optimum für die Prozessorzahl, das bestenfalls experimentell bestimmbar ist.
Ansätze
Die Rechenarbeit wird auf mehrere Kerne einer Maschine verteilt durch
- ausdrückliches Multithreading (POSIX / Boost / C++11 <thread>),
- implizites Multithreading in OpenMP, Parallel Pattern Library (Microsoft Visual C++ 2010) und Thread Building Blocks (Intel C++),
Stehen mehrere Maschinen zur Verfügung, kommen
- allgemeine verteilte Systeme (Client/Server-Anwendungen über Netzwerk-Sockets, CORBA, …) und
- Message Passing Interface (Open MPI) als Grundlage für Supercomputer-Cluster
zum Einsatz.
Beispiele
Um einen Eindruck zu gewinnen, wurde dieselbe Programmieraufgabe (Berechnung eines Apfelmännchens) mit mehreren Techniken umgesetzt; die Ausgabe des Rechenergebnisses als Bilddatei (Abb. rechts) erlaubt ein leichtes Erkennen von Fehlern:
Einschätzung
Die Tabelle fasst die gemachten Erfahrungen zusammen:
| Technik | Programmieraufwand | Compiler | Einschränkungen, Abhängigkeiten | erreichte Beschleunigung1) | |
|---|---|---|---|---|---|
| OpenMP | Pragmas, geteilte Schleifen | minimal, auch seriell | GCC, Visual C++ ≥2005 | OpenMP-Bibliothek | 2,1 |
| PPL | Templates, Lambdas, Threadpool | gering | Visual C++ 2010 | 1,9 | |
| OpenCL | Rechenkerne in C | hoch | GCC, Visual C++ 2010 | Grafikkarte, Treiber, ATI-Stream-Software, nicht alle Datentypen nutzbar | 15 |
| Open MPI | Bibliothek | hoch | GCC, Linux | ssh-Zugriff auf alle beteiligten Maschinen | — |
OpenMP und MPI weisen die größte Reife auf und können ergänzend genutzt werden, MPI ist auf Rechnerclustern skalierbar. OpenCL ist noch relativ jung und wegen der Abhängigkeit von Fähigkeiten der Grafikkarte und weiterer Software noch wenig portabel, verspricht aber bei vielen Grafikkernen große Geschwindigkeitsgewinne.
Weitere Messungen wurde an Udoo Quad durchgeführt.