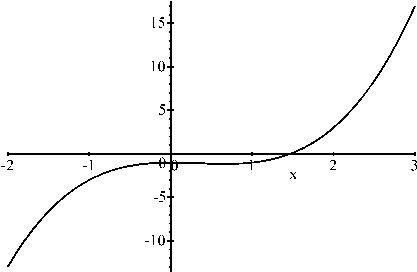Grau, bester Freund, ist alle Theorie.

— Goethe : Faust I

Ein Algorithmus ist im weitesten Sinne eine ausführbare Vorschrift, deren einzelne Schritte in ihrer Reihenfolge genau festgelegt sind. Algorithmen gibt es in vielen Bereichen. Hier werden nur einige Rechenalgorithmen als Beispiele genutzt.

Algorithmen lassen sich automatisieren. Dazu muss der Algorithmus in einer bestimmten, von der Maschine ausführbaren Form niedergeschrieben werden: als Programm.

Einer der ältesten Algorithmen [Heron von Alexandria, um 75 u.Z.] berechnet die Quadratwurzel einer Zahl $a$:

  Beginne mit einem Rechteck der Fläche a x 1 (Seitenlängen a und 1).
  Solange beide Seiten voneinander verschieden sind,
      bilde das arithmetische Mittel m beider Seitenlängen,
      neue Seitenlängen sind m und und der Quotient aus a und m. 

Die Form des Rechtecks nähert sich dabei immer mehr einem Quadrat an. Im Grenzfall (nach unendlich vielen Rechenschritten) sind beide Rechteckseiten gleich lang. Die Quadratwurzel von $a$ ist dann $x = \sqrt{a}$ mit der Eigenschaft $x \cdot x = a$.

Praktisch wird niemand unendlich viele Schritte durchführen — aus zwei Gründen:

1. Keiner hat unendlich viel Zeit. Deshalb begnügt man sich mit einem Näherungswert. Die Rechnung wird beendet, wenn die Differenz der Seitenlängen innerhalb einer vertretbaren Toleranz liegt.
2. Dieser Toleranzwert kann in Computerprogrammen auch nicht beliebig verkleinert werden. Dezimalzahlen mit gebrochenem Anteil werden nur mit beschränkter Genauigkeit gespeichert. Typisch sind etwa 6 bis 20 gültige Ziffern, je nach Rechner und Programm.

Dieser Algorithmus liefert nur einen Näherungswert. Allerdings kann das Intervall angegeben werden, in dem die genaue Lösung liegt: $[a/m, m]$.

Formale Beschreibungen sind meist kürzer und präziser als umgangssprachliche:

  // Quadratwurzel aus a nach Heron:
  x = a; y = 1;
  Solange x > y
      x = (x+y)/2
      y = a/x
  // Ergebnis: x = Quadratwurzel von a 

Dieser Algorithmus liefert die Quadratwurzel für jeden beliebigen Wert a, solange dieser größer oder gleich 1 ist. Sollen auch Wurzeln von Zahlen kleiner 1 gebildet werden, sind vor der Schleife x und y zu vertauschen. Die Umsetzung in C++ kann so aussehen:

#include <algorithm> // swap()
 
double square_root(double a) 
{
  double x = a, y = 1;
  if (x < y) std::swap(x, y); // falls 0 <= a < 1
  while (x > y) 
  {
    x = (x+y)*0.5;
    y = a/x;
  }
  return x;
}

Der Algorithmus versagt immer noch für negative Zahlen a: Praktisch kommt er hier nicht zum Ende (bleibt in der Schleife hängen) oder erzeugt einen fatalen Fehler (stürzt mit Division durch Null ab).

Algorithmen müssen drei Bedingungen erfüllen:

1. Sie müssen aus zweifelsfrei aufeinanderfolgenden Anweisungen bestehen (eindeutig sein).
2. Sie müssen zu einem Ergebnis führen (effektiv sein).
3. Sie müssen stets zum richtigen Ergebnis führen (korrekt sein).

Für praktikable Algorithmen folgen daraus einige Einschränkungen:

1. Das Programm darf nicht in einer Endlosschleife hängenbleiben.
2. Bestimmte Algorithmen übersteigen in Speicherbedarf und/oder Rechenzeitbedarf die Grenzen verfügbarer Rechner oder auch des Universums, obwohl sie in beiden Forderungen endlich sind.
3. Sie sollten das Ergebnis mit möglichst geringem Aufwand (an Rechenzeit und Speicherbedarf) erreichen (effizient sein).
4. Einschränkungen hinsichtlich der Startwerte sollten klar dokumentiert sein. Der Start mit ungültigen Werten sollte unmöglich gemacht oder wenigstens mit einer Fehlermeldung versehen werden.

Zusicherungen (Tests von Vor- bzw. Nachbedingungen) können fehlerhafte Ergebnisse verhindern helfen. Schlägt der Test fehl, wird das Programm beendet, wie im Beispiel einer "sicheren" Wurzelfunktion:

#include <cassert>
 
double square_root(double a) 
{
  assert(a >= 0);
  // ... wie oben
}

Ebenso könnte eine andere Aktion ausgelöst werden (Auswurf einer Ausnahmebedingung in ANSI C++ oder Ausgabe einer Fehlermeldung auf Bildschirm oder in Datei).

Funktionen mit eingeschränktem Definitionsbereich können in Funktionen eingebaut werden, die den Definitionsbereich erweitern, Vorabtests durchführen etc. Ein Algorithmus ggT(a, b) für den größten gemeinsamen Teiler von $a$ und $b$ funktioniert nur für $a,b \geq 0$. Am ggT ändert sich nichts, wenn die Beträge genommen werden:

long ggT_sicher(long a, long b) 
{
  if (a < 0) a = -a;
  if (b < 0) b = -b;
  return ggT(a, b);
}

So braucht die Betragsbildung nur einmal, beim ersten Aufruf erfolgen. Damit werden unnötige Tests vermieden, z. B. falls ggT(a, b) rekursiv definiert wurde.

Algorithmen für spezielle Aufgaben sind vielfach schneller ausführbar als allgemeinere, denn sie können bestimmte zusätzliche Eigenschaften des zu bearbeitenden Problems für Abkürzungen ausnutzen — sind manchmal aber gerade deshalb schwerer verständlich.

Der Korrektheitsnachweis für Algorithmen ist selbst nicht algorithmisierbar. Das ist eine Folge einer fundamentalen mathematischen Aussage, des Gödelschen Unvollständigkeitssatzes. Praktisch bedeutet das: Ein Compiler findet nicht alle Fehler, da er Programme nicht verstehen, sondern nur abarbeiten kann. Die Bedeutung eines Programms oder Quelltextes ist der Maschine unzugänglich. So können z. B. Endlosschleifen unerkannt bleiben. Ein allgemein gehaltenes Testprogramm kann nur bejahen, dass eine Schleife zum Ende kommt, indem es sie durchläuft und das Ende erreicht. In Endlosschleifen bleibt es hängen und kommt deshalb nie zum Ergebnis (in der Informatik als Halteproblem bezeichnet).

Wird der Korrektheitsnachweis nicht mit mathematischer Strenge geführt, bleiben nur Testläufe als Hilfe. Um wirklich sicher zu gehen, müsste ein Algorithmus mit allen möglichen Startwerten getestet werden. Auch das ist meist (aus Zeitgründen) unmöglich.

Große Programme bestehen aus vielen kleineren Teilen, die zusammenwirken und aufeinander aufbauen. Das folgende Beispiel ist anschaulich, aber nicht praktisch. Es erklärt, wie die Grundrechenarten für natürliche Zahlen von Grund auf erklärt werden können. Zur Erinnerung: Eine natürliche Zahl bezeichnet die Anzahl der Elemente in (irgendeiner) Menge, z. B. eines Haufens mit Baumstämmen.

Durch Hinzufügen oder Wegnehmen eines Elementes der Menge erhöht bzw. vermindert sich die natürliche Zahl um eins. Es entstehen Nachfolger und Vorgänger der Zahl. Für jede natürliche Zahl $n$ gibt es genau einen Nachfolger

succ(n) = n+1

und für jede positive natürliche Zahl $n > 0$ genau einen Vorgänger

pred(n) = n-1.

Das Zusammenfügen zweier Mengen kann nun so durchgeführt werden:

  Solange in der zweiten Menge noch Elemente sind,
      nimm ein Element heraus und füge es der anderen Menge hinzu. 

Mit Rechensteinen wurden auf diese Weise zwei Zahlen $a$ und $b$ addiert:

  // Addieren von a und b:
  s = a
  Solange b > 0 ist,
      vermindere b um eins und erhöhe s um eins.
  // Ergebnis: Die Summe von a und b ist das neue s. 

Durch wiederholtes Addieren von $b$ lässt sich das Vielfache einer Zahl $a$ bilden:

  // Multiplizieren von a und b:
  p = 0
  Solange b > 0 ist,
      bilde den Vorgänger von b und addiere a zu p.
  // Ergebnis: Die Produkt von a und b ist das neue p. 

Eine Potenz $a^n$ erhält man durch wiederholtes Multiplizieren:

  // n-te Potenz von a:
  p = 1
  Solange n > 0 ist,
      bilde den Vorgänger von n und multipliziere p mit a.
  // Ergebnis: Die Potenz an ist das neue p. 

Nun könnte man die Algorithmen als Programme niederlegen:

unsigned long add(unsigned long a, unsigned long b) 
{
  while (b--) a++;
  return a;
}
 
unsigned long mult(unsigned long a, unsigned long b) 
{
  unsigned long p = 0;
  while (b--) p = add(p, a);
  return p;
}
 
unsigned long power(unsigned long a, unsigned long n) 
{
  unsigned long p = 1;
  while (n--) p = mult(p, a);
  return p;
}

Das Zeitverhalten dieses Beispiels ist jedoch scheußlich:

• Das Addieren dauert umso länger, je größer der zweite Summand ist. add(1000, 1) und add(1, 1000) dauern unterschiedlich lange.
• Multiplizieren dauert umso länger, je größer das Produkt ist.
• Auf das Ergebnis von power(10, 9) kann man (je nach Rechner) zwischen einer Stunde und einem Vierteljahr warten.

Die Komplexität oder Ordnung eines Algorithmus kennzeichnet, wie sich der Lösungsaufwand für Probleme wachsender Größe ändert. Die Problemgröße $n$ kann dabei der Wert von Parametern oder die Anzahl zu verarbeitender Daten sein.

• Wird in einer ungeordneten $n$-elementigen Menge ein bestimmtes Element gesucht, müssen im Mittel $n/2$ Elemente untersucht werden. Die Suchzeit ist proportional zu $n$. Der Suchalgorithmus hat lineare Komplexität, ist von der Ordnung $O(n)$.
• Ist die Menge geordnet, kann ein effizienteres Suchverfahren eingesetzt werden: Bei binären Suchverfahren ist das Ansteigen des zeitlichen Aufwands nur logarithmisch, von der Ordnung $O(\log n)$.
• Das Sortieren von $n$ Elementen einer Menge geschieht am einfachsten, indem erst das kleinste Element gesucht und dann aus der Menge herausgenommen wird. Dann kommt das nächstkleinste Element der Restmenge dran (Selection Sort). Der Aufwand ist von der Ordnung $O(n^2)$, d. h. bei Verdopplung der Anzahl der Elemente vervierfacht sich die Sortierzeit. Das bedeutet quadratische Komplexität.
• Effizentere Sortierverfahren sind von der Ordnung $O(n \log n)$, z. B. Quick Sort und Heap Sort.
• Das Multiplizieren $n$-reihiger quadratischer Matrizen ist von der Ordnung $O(n^3)$. Eine Verdopplung der Reihenanzahl zieht eine Verachtfachung des Rechenaufwands nach sich, da drei ineinandergeschachtelte Schleifen durchlaufen werden müssen.
• Das Zeit für das Umschichten des Turmes von Hanoi verdoppelt sich mit jeder hinzukommenden Scheibe. Nach buddhistischen Vorstellungen ist das Weltenende erreicht, ehe die Aufgabe bewältigt ist. Dieses Problem ist von der Ordnung $O(2^n)$. Primzahltests erfordern ebenfalls Algorithmen von exponentieller Komplexität. Nur deshalb lassen sich Verschlüsselungsverfahren angeben, an denen auch die größten Rechenanlagen heute noch scheitern, so dass die Botschaften geheim bleiben.
• Das Problem des Handlungsreisenden - die kürzeste Reiseroute durch $n$ Orte - und das Rucksackproblem - die Auswahl der wertvollsten Gegenstände bei begrenztem Packvolumen - ist von noch größerer, kombinatorischer Komplexität: Ordnung $O(n!)$.

Eine ganze Anzahl von Problemen sind bekannt, für die bisher kein deterministisches Lösungsverfahren von polynomialer Laufzeit $O(n^k)$ gefunden wurde (sog. NP-harte Probleme). Allerdings gibt es einen mathematischen Satz, nach dem alle diese Probleme polynomial sind, falls ein polynomialer Algorithmus für eines dieser Probleme gefunden wird. Die Chancen dafür stehen allerdings ziemlich schlecht.

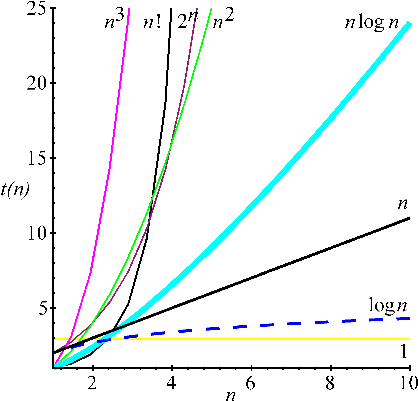
Abb.1 Zeitverhalten von Algorithmen unterschiedlicher Komplexität

Das Diagramm 1 zeigt, wie schnell der zeitliche Aufwand für Algorithmen unterschiedlicher Ordnungen bei wachsender Problemgröße anwächst. Ist die Rechenzeit vorgegeben (als waagerechte Linie), bringt ein Wechsel zu einem schnelleren Algorithmus wesentlich mehr als lokale Optimierungen. Wächst die Komplexität schneller als $n$, nützt auch die Anschaffung eines 10mal schnelleren Rechners wenig — der zudem meist noch mehr als 10mal teurer ist.

Ein Algorithmus gilt als "schnell", wenn seine Ordnung $O(\log n)$ nicht übersteigt. Doch Vorsicht! Diese Angabe eignet sich nicht, unterschiedliche Algorithmen zu vergleichen. Für kleine Werte $n$ kann durchaus ein "schlechter" Algorithmus überlegen sein, wenn er pro Einzelschritt wesentlich schneller ist. Die Implementierung von Sortierverfahren kann z.B. Quick Sort verwenden und bei kleinen Datenmengen auf Selection Sort umschalten.

Ein "schneller" Algorithmus zur Matrizenmultiplikation (STRASSEN) ist von der Ordnung $O(n^{2.807})$ statt $O(n^3)$. Der Vorteil wird allerdings erst bei Problemgrößen wirksam, die jenseits der Beschränkungen heutiger Computer liegen — wobei nur Multiplikationen und Additionen eingerechnet sind. "Kleinigkeiten" wie die benötigte Zeit für Speicherzugriffe und Parameterübergaben werden großzügig übergangen. Auch das ist ein Grund für die Kritik in [NumRecipes, S. 25]:

One of the cultural barriers that separates computer scientists from "regular" scientists and engineers is a differing point of view on whether a 30% or 50% loss of speed is worth worrying about. In many real-time or state-of-the-art scientific applications, such a loss is catastrophic. The practical scientist is trying to solve tomorrow's problems with yesterday's computer; the computer scientist, we think, often has it the other way round.

The German mathematician Kronecker, sitting quietly at his desk, wrote:
God created the whole numbers, all the rest is man's work.
Seated in front of the terminal, with Basic hanging on my every keystroke, I typed:
for i=1 to infinity
__ let number[i]=i

— Leslie Lamport [LaTeX. A document preparation system. S. 5]

Zwei Konzepte widerstreiten, wie man zu einem bestimmten Ergebnis kommt.

• Iteration (lat. Wiederholung) durchläuft eine Rechenfolge in einer Schleife, bis das gewünschte Ergebnis erreicht ist. Paradebeispiel ist die Definition der Fakultätsfunktion:

$$n! = 1\cdot 2\cdot\ldots…\cdot n.$$

• Rekursion (lat. Zurückführung) führt einen Zusammenhang auf einen einfacheren zurück, bis der Anfang (die Abbruchbedingung) erreicht ist. Man "zäumt hier das Pferd von hinten auf":

$$ n! = \begin{cases} n \cdot (n-1)! & \text{für } n > 0, \\ 1 & \text{für } n = 0. \end{cases} $$ Jede Iteration lässt sich auf einfache Weise auch als Rekursion auffassen, indem man hinten anfängt. Umgekehrt kann aber nicht jede Rekursion in eine Iteration umgewandelt werden. Rekursion ist allgemeiner als Iteration. Die Hypothese von Church besagt:

  Alles, was sich rekursiv definieren lässt, ist berechenbar, kann also von einem Computer ausgeführt werden. 

Der rekursive Abstieg birgt auch Gefahren:

• Auf jeder Rekursionsstufe müssen Zwischenwerte bewahrt und Funktionsparameter übergeben werden. Bei zu vielen Rekursionsschritten und zu vielen Werten läuft der Zwischenwertspeicher (Stapel) über.
• Ein fehlender oder fehlerhafter Abbruchwert führt zu Endlosrekursion (d.h. praktisch zum Stapelüberlauf), wie im Kinderreim:

Ein Mops kam in die Küche und stahl dem Koch ein Ei.
Da nahm der Koch die Kelle und schlug den Mops zu Brei.
Da kamen viele Möpse und gruben ihm ein Grab und setzten einen Grabstein,
auf dem geschrieben stand: … [wieder von vorn]

Bei rekursiv definierten Algorithmen muss wie bei Schleifen sichergestellt werden, dass sie zum Ende kommen. Die Fakultät darf nur von natürlichen Zahlen $n \geq 0$ berechnet werden. Die rekursiv definierte Funktion $$ f(x) = \begin{cases} 1 & \text{für } x = 1,\\ 2+f(x-2) & \text{für } x > 1. \end{cases} $$ liefert nur für ungerade Funktionswerte $x$ ein Ergebnis, für gerades $x$ führt die Berechnung zum Absturz. Bei der Funktion von Hasse-Kakutani-Syracuse $$ f(x) = \begin{cases} 1 & \text{für } x = 1,\\ f(x/2) & \text{für gerades } x,\\ f(3x+1) & \text{für ungerades } x. \end{cases} $$ ist ungeklärt, ob sie für jeden Funktionswert $x > 0$ zum Ende kommt. (Experimente bis $x = 2^{29}$ liefen erfolgreich). Die Anzahl der Rekursionsschritte dieser Funktion in Abhängigkeit vom Startwert definiert die Collatz-Folge

1 1 7 2 5 8 16 3 19 6 14 …,

deren Werte keine Regelmäßigkeit erkennen lassen.

Ruft eine Funktion über eine andere sich wieder selbst auf, entsteht indirekte Rekursion. Der wechselseitige Aufruf von Algorithmen ist besonders schwer zu erkennen, wenn er über mehrere Zwischenschritte erfolgt. Im Spaß:

  Die rechte Hand ist die, wo der Daumen links ist. (Für links umgekehrt.) 

Im Ernst:

  Eine Zahl ist ungerade, wenn sie nicht gerade ist.
  Eine positive Zahl ist dann gerade, wenn ihr Vorgänger ungerade ist.
  Null ist gerade. 

Als Quelltext:

bool even(int x); //  forward-Deklaration notwendig!
 
bool odd(int x)  { return !even(x); }
bool even(int x) { return x == 0 ? true : odd(x-1); }

Effizientere Algorithmen lassen sich im Wesentlichen durch folgende Maßnahmen erreichen:

• Umwandeln rekursiver Berechnungen in iterative,
• algebraische Umformungen,
• Reduzieren der Komplexität (Teile-und-herrsche-Strategien),
• veränderte (allgemeinere) Fragestellung,
• lokale Optimierungen.

Die baumartige Verzweigung der rekursiv definierten Fibonacci-Funktion

long fibonacci(long n) 
{
  if (n < 2) return n;
  return fibonacci(n-2) + fibonacci(n-1);
}

erzeugt $F_n$ Funktionsaufrufe! Der Rechenaufwand steigt exponentiell: $O(1.618^n)$. Die Funktion lässt sich auch iterativ abarbeiten, wozu bereits berechnete Fibonaccizahlen Fn in einem Feld abgelegt werden können. Da bei $n > 46$ sowieso ein Ganzzahl-Überlauf erfolgt, kann eingeschränkt werden.

long fibonacci(long n) 
{
  int const max = 47; // mehr geht nicht - Overflow !
  long f[max];
  assert(n < max);
 
  f[0] = 0; f[1] = 1;  // Startwerte
  for (long i = 2; i < n; ++i) f[i] = f[i-1] + f[i-2];
  return f[n];
}

Dieser Algorithmus besitzt nur linearen Aufwand $O(n)$. Auf das Feld kann sogar verzichtet werden, da immer nur die zwei vorhergehenden Werte benötigt werden:

long fibonacci(long n) 
{
  long a = 0, b = 1;
  for (long i = 2; i < n; i++) {
    b += a; a = b-a;
  }
  return a + b;
}

Für die Fibonacci-Zahlen $F_n$ gilt die (nicht ohne weiteres ersichtliche) Matrizengleichung $$ \left( \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right)^n = \left( \begin{matrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{matrix} \right), $$ aus der sich weitere rekurrente Beziehungen herleiten lassen: $$ \begin{align} F_{n+1}F_{n-1}-F_n^2 & = (-1)^n \qquad\qquad \text{(CASSINIsche Formel)}, \\ F_{m+n} &= F_m F_{n+1}+F_{m-1} F_n, \\ F_{2n+1} &= F_n^2+F_{n+1}^2 \qquad \text{(Verdopplungsformeln)}, \\ F_{2n+2} &= 2F_n F_{n+1}+F_n^2. \end{align} $$ Der Potenzmatrix-Algorithmus kann dieselbe Komplexität $O(\log n)$ wie ein schneller Potenzierungsalgorithmus besitzen. Die Anwendung der Verdopplungsformeln verfolgt dieselbe Teile-und-herrsche-Strategie wie die ägyptische Bauernmultiplikation mit Ordnung $O(\log n)$.

Einen direkten Zugang zu den Fibonacci-Zahlen liefert die Formel von Binet: $$ F_n = 1/\sqrt 5 \cdot \left\lbrace [(1 + \sqrt 5) / 2]^n - [(1 - \sqrt 5) / 2]^n \right\rbrace. $$ Der Term $[(1-\sqrt 5) / 2]$ ist betragsmäßig kleiner 1 und strebt bei fortgesetztem Potenzieren gegen Null. Es genügt hier, die erste Potenz auszuwerten und dann zur nächstliegenden Ganzzahl zu runden. Diese Berechnung ist von der Ordnung $O(1)$ und liefert das Ergebnis in konstanter Zeit. Allerdings muss man sich hier auf die Genauigkeit von Gleitkommazahlen verlassen:

#include <cmath> // sqrt(), pow()
 
long fibonacci(long n) 
{
  double w = std::sqrt(5);
  return pow((1 + w)*0.5, n)/w + 0.5; // implizite Rundung
}

Diese Strategie römischer Feldherren führt auch hier zum Erfolg.

Ein bestimmtes Element x vom Typ T in einer aufsteigend geordneten Menge (Feld a[lo…hi] oder Binärbaum) lässt sich mit logarithmischem Aufwand $O(\log n)$ finden:

int binsearch(int lo, int hi, T x, T a[]) 
{
  while (lo < hi) 
  {
    int m = (lo+hi)/2;
    if (x == a[m]) return m;
    if (x < a[m]) hi = m-1; else lo = m+1;
  }
  return -MAXINT; /* nicht gefunden */
}

Führt lokales Optimieren zu klarerem Quellcode, ist es immer zu befürworten. Aufwand und Nutzen müssen jedoch in einem vernünftigen Verhältnis stehen.

Ansonsten ist dies erst sinnvoll, wenn aus dem optimalen Algorithmus das letzte Quentchen Geschwindigkeit herausgeholt werden soll. Dabei sollten nur die innersten Schleifen optimiert werden, in denen das Programm sich am längsten aufhält. Nur dort besteht Aussicht auf einen merklichen Geschwindigkeitszuwachs. Um die für Optimierungen geeigneten Stellen zu finden, ist ein Profiler hilfreich. Gibt es keinen solchen, tun es zur Not auch Bildschirmausschriften an verdächtigen Stellen (poor man's debugger). Manche Compiler führen solche Optimierungsaufgaben auch automatisch durch (optimierende Compiler).

Constant propagation berechnet Konstanten schon beim Übersetzen. Anstelle von a = 2; b = a+3; kann a = 2; b = 5; geschrieben werden. Die Anweisungen

a = x; b = 0; c = a/x;
d = x*c; e = x+b;

können vereinfacht werden zu

b = 0; c = 1; a = d = e = x; // fortlaufende Zuweisungen

Common subexpression elimination nimmt aus

x = (a+b + abs(a-b))/2;
y = (a+b - abs(a-b))/2;

gemeinsame Teilausdrücke heraus:

u = a+b;
v = abs(a-b);
x = (u+v)/2;
y = (u-v)/2;

Reducing operator strength ersetzt Divisionen oder Multiplikationen mit Potenzen von 2 bei Ganzzahlen durch schnellere Bitschiebeoperationen:

x = a*4;  y = a/8;
x = a<<2; y = a>>3; /* Bitschieben nach links/rechts */

Statt x = pow(a,4); lässt sich auch x=a*a; x*=x; schreiben.

Copy propagation verändert x = a+b; c = a; y = c+b; zu c = a; x = y = a+b;.

Invariant code motion entfernt invariante Terme aus Schleifen. Aus

for (i = 0; i < 100; i++) a[i] = x+y;

kann die Summe x+y als Hilfsvariable t herausgenommen werden:

for (i = 0, t = x+y; i < 100; i++) a[i] = t;

Loop strength reduction ersetzt z.B. wiederholte Multiplikationen

for (i = 0; i < 100; i++) a[i] = 4*i;

durch fortgesetzte Additionen

for (i = 0, t = 0; i < 100; i++, t += 4) a[i] = t;

Loop jamming fasst mehrere Schleifen

for (i = 0; i < 100; i++) a[i] = 0;
for (i = 0; i < 100; i++) b[i] = a[i]+x;

zu einer zusammen:

for (i = 0; i < 100; i++) { a[i] = 0; b[i] = x; }

Optimierte Speicheradressierung (d.h. die Ausnutzung von Zeigern und ihrer Arithmetik) bringt bei

for (i = 0; i < 100; i++) a[i] = x;

ebenfalls Gewinne:

int *pa = a, *pEnd = a+100;
while (pa < pEnd) *pa++ = x;

Adressen sollten nur so oft wie notwendig ausgewertet werden. Dem tragen die Kurzschreibweisen für Verbundzuweisungen und Inkrement-/Dekrement-Operatoren Rechnung, die C so "unleserlich" machen:

x *= ++y + 2; // y = y+1; x = x*(y+2);

Schleifenzähler oder temporär genutzte Werte können ohne Zuhilfenahme des langsamen Hauptspeichers in Prozessorregistern gehalten werden. Hier sollte man dem Compiler allerdings nicht ins Handwerk pfuschen.

Ganzzahlen statt Gleitkommawerte können zu einer Beschleunigung führen, wenn Gleitkommaoperationen langsamer sind oder vom Prozessor emuliert werden müssen (Faktor 20). Es soll jedoch Rechner geben (z. B. CRAY), bei denen das genau anders herum ist!

Doppelt genaue Gleitkommazahlen (8 Byte) werden langsamer verarbeitet, wenn die Prozessorregisterbreite oder die Speicherbusbreite zu eng ist, z.B. nur vier (x386), zwei (x286) oder ein Byte (8088) beträgt. Die Berechnung von float-Zahlen (vier Byte) profitiert stark von x386-(32Bit-)Code-Compilern (Faktor 10 bei Emulation).

Multiplikationen sind langsamer als Additionen (etwa Faktor 3), Divisionen sind noch langsamer (etwa Faktor 8). Deshalb sollten wiederholte Divisionen von Gleitkommazahlen soweit als möglich durch Multiplikationen ersetzt werden.

Theoretisch stimmen Theorie und Praxis überein, praktisch nicht.

— Jan L.A. van de Snepscheut

Dieser Abschnitt enthält eine Auswahl von Algorithmen, wobei auf Vor- und Nachteile bestimmter Implementierungen eingegangen wird. Die optimale Umsetzung ist immer an bestimmte Schwerpunkte geknüpft.

Das Multiplizieren großer natürlicher Zahlen $m$ und $n$ lässt sich nach folgendem Algorithmus ausführen:

  Solange n > 0,
      wenn n ungerade, addiere m zum Ergebnis.
      Verdopple m und halbiere n (ohne Rest). 

Diese Multiplikation von der Ordnung $O(\log n)$ ist ein hervorragendes Beispiel für die Teile-und-herrsche-Strategie. Das schriftliche Multiplizieren von Dezimalzahlen funktioniert übrigens genauso, nur mit dem Faktor 10.

unsigned egyptian_product(unsigned m, unsigned n) 
{
  unsigned p = 0;
  for (; n > 0; m <<= 1, n >>= 1) if (n % 2) p += m;
  return p;
}

Schnelles Potenzieren mit natürlichem Exponenten verfolgt die gleiche Strategie mit O(log n). Für das Potenzieren z.B. von Matrizen muss ebenfalls ein solcher Algorithmus verwendet werden.

double power(double x, unsigned int n) 
{
  double p = 1;
  for (; n > 0; x *= x, n >>= 1) if (n % 2) p *= x;
  return p;
}

Für Potenzen mit reellwertigen Basen und Exponenten ist allerdings schon die Funktion std::pow(base, exp) mit dem maximal möglichen Definitionsbereich in <cmath> vordefiniert. Es lohnt sich nicht, das Rad nochmal zu erfinden.

Der größte gemeinsame Teiler (ggT) zweier ganzer Zahlen $a,b \in Z$ besitzt die folgenden Eigenschaften:

ggT(a,b) = ggT(b,a)
ggT(a,b) = ggT(-a,b)
ggT(a,0) = |a| .

Wegen der zweiten Gleichheit kann man sich auf natürliche Zahlen beschränken. Ist $t$ ein gemeinsamer Teiler von $a$ und $b$, so teilt $t$ auch ihre Summen, Differenzen und beliebige Vielfache: $$ t | a \wedge t | b \Rightarrow t | ax \pm by. $$ Diese Eigenschaften genügen, um das ggT durch wiederholte Anwendung von

ggT(a,b) = ggT(a-b,b) = ggT(a mod b,b) =	ggT(b, a mod b).

zu bestimmen (für $a > b > 0$ gilt stets $b > (a\mod b)$). Die Zahlen werden dabei immer kleiner. Das Verfahren endet, wenn das rechte Argument 0 ist. Die rekursive Implementierung folgt unmittelbar daraus:

long ggT_rec(long a, long b) 
{
  if (b == 0) return a < 0 ? -a : a;
  return ggT_rec(b, a % b);
}

Sie ist auch für negative Zahlen gültig. Man kann sich an einem Beispiel veranschaulichen, wie dieser Algorithmus von EUKLID (365-309 v. Chr.) abläuft, um eine iterative Version abzuleiten:

a   b   a mod b
36  28  8
  /   /
28  8   4
  /   /
8   4   0
  /   /
4   0      ggT(36,28) = 4

long ggT(long a, long b) 
{
  long r = b;
  while (r) { r = a % b; a = b; b = r; }
  return a < 0 ? -a : a;
}

Beide Versionen des Algorithmus sind von der Ordnung $O(\log n)$.

Durch das überexponentielle Ansteigen der Funktionswerte ($12! = 4.79\cdot 10^8$) hat eine Umsetzung der Funktion in Ganzzahlarithmetik wenig Sinn. Für den Rückgabewert müssen Gleitkommawerte zur Verfügung gestellt werden. Allerdings kann auch mit double-Arithmetik maximal $170! = 7.2574\cdot10^{306}$ berechnet werden. Beim nächsten Wert kommt es zum Gleitkommaüberlauf (Programmabbruch). Wird die Fakultätsfunktion in einem Programm häufig eingesetzt, lassen sich bereits errechnete Werte als Feld a[n] speichern und dann schnell abrufen.

double factorial(int n) 
{
  int const nmax = 170;
  static int ntop = 0;
  static double a[nmax+1] = {1.0}; // 0! = 1
 
  assert(0 <= n && n <= nmax);
 
  while (ntop < n) 
  {
    int j = ntop++;
    a[ntop] = a[j] * ntop;
  }
  return a[n];
}

In der Kombinatorik werden häufig Fakultäten sehr großer Zahlen miteinander multipliziert und dividiert, mit recht "gewöhnlichen" Ergebnissen. Üblich ist, so etwas durch Addieren bzw. Subtrahieren der Logarithmen zu erledigen, um den Gleitkommaüberlauf zu vermeiden. Dazu kann auch der natürliche Logarithmus der Fakultät benutzt werden. Dazu wird die Beziehung $n! = \Gamma(n+1)$ zur Gamma-Funktion benutzt.

float log_Gamma(float x); // ln(Gamma(x)) siehe unten
 
float log_factorial(int n) 
{
  assert(n >= 0);
  return log_Gamma(n+1); // ln(n!)
}

Wieviel Möglichkeiten gibt es, 6 Zahlen aus 49 auszuwählen? Die Antwort ist $\binom{49}{6} = \frac{49\cdot 48\cdot 47\cdot 46\cdot 45\cdot 44} {1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6} = 13983816$. Der Kehrwert dieser Zahl ist die Wahrscheinlichkeit eines Sechsers im Lotto. So bleibt zum Glückspiel nur zu sagen: Let it be. Die Berechnung des Binomialkoeffizienten $$ \binom{n}{k} = \frac{n!}{k!\cdot (n-k)!} \text{ mit } 0 \leq k \leq n $$ (gesprochen: n über k) ist auf mehrere Arten möglich. Eine direkte Variante mit Ganzzahlen liefert wegen eines Überlaufs schon bei 100 über 6 fehlerhafte Ergebnisse. Deshalb muss der Rückgabewert eine Gleitkommazahl sein:

double binomial(int n, int k) 
{
  double p = 1;
  if (k > n/2) k = n-k;
  for (int i = 1; i <= k; n--, i++) p = p*n/i;
  return p;
}

Für große $n$ und $k \approx n/2$ kostet die Berechnung jedoch viel Zeit. Auch der Rückgriff auf die Fakultät ist möglich, beschränkt jedoch $n \leq 170$:

double binomial(int n, int k) 
{
  return std::floor(factorial(n)/(factorial(k)*factorial(n-k)) + 0.5);
}

Am Ende wird mit floor(x+0.5) gerundet. Eine dritte Variante nutzt $\ln n!$:

double binomial(int n, int k) 
{
  return std::floor(std::exp( log_factorial(n)
                             -log_factorial(k)-log_factorial(n-k))+0.5);
}

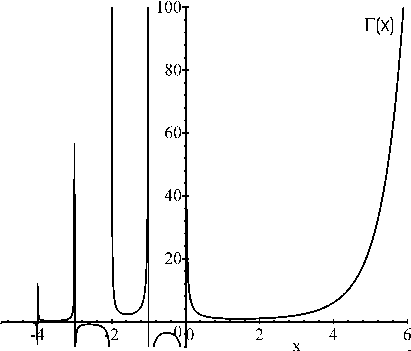
Eine wichtige "spezielle" Funktion, die Gamma-Funktion, wird durch das Integral $$ G(x) = \int_1^\infty t^{x-1}e^{-t}dt $$ definiert. Sie kann wegen $\Gamma(n+1) = n!$ als Erweiterung der Fakultät auf die reellen Zahlen angesehen werden. Sie erfüllt ebenso wie die Fakultät die Rekurrenzbeziehung $\Gamma(z+1) = z\cdot \Gamma(z)$. Die Funktion ist im positiven Bereich stetig und besitzt bei 0 und allen negativen ganzzahligen Werten $z$ Pole (siehe Abb. 2).

Abb. 2: Die Gammafunktion G(x).

Die Funktion liegt gewöhnlich in Tabellenform für $x \geq 1$ vor oder wird durch eine Reihe approximiert. Wegen ihres steilen Anstiegs im positiven Bereich wird der Logarithmus der Funktion implementiert [NumRecipes S. 214]. Intern ist sie nicht komplexer als die in den numerischen Koprozessor "eingegossenen" Funktionen wie $\sin(x)$ oder $e^x$:

#include <cmath>
 
float log_Gamma(float xx) // ln Gamma(xx) mit xx > 0 
{
  int j;
  double x,y,tmp,ser;
  static double cof[6] = {76.18009172947146,     -86.50532032941677,
                          24.01409824083091,     -1.231739572450155,
                          0.1208650973866176e-2, -0.5395239384953e-5};
  y = x = xx;
  tmp = x + 5.5;
  ser = 1.000000000190015;
  tmp -= (x+0.5) + log(tmp);
  for (j = 0; j <= 5; j++) ser += cof[j]/++y;
  return -tmp + std::log(2.5066282746310005*ser/x);
}

Eindrucksvoll, nicht wahr? Intern wird doppelte Genauigkeit benutzt, um float-Genauigkeit des Funktionswertes zu sichern.

Die bei Informatikern beliebte Ackermann-Funktion (1928) $$ Ack(x,y) = \begin{cases} y+1 & \text{für } x = 0 \\ Ack(x-1, 1) & \text{für } y = 0 \\ Ack(x-1, Ack(x, y-1) ) & \text{sonst.} \end{cases} $$ wurde erfunden, um zu beweisen, dass es Funktionen gibt, deren Rekursion nicht primitiv ist. Ihr Parameter $x$ legt fest, welche Grundrechenart auf $y$ angewandt werden soll: $$ \begin{align} Ack(0, y) &= y+1\\ Ack(1, y) &= y+2\\ Ack(2, y) &= 2y+3\\ Ack(3, y) &= 2^{y+3}-3\\ Ack(4, y) &= 2^{2^{\cdot ^{\cdot ^{\cdot ^2}}}}-3 . \end{align} $$ Der Exponententurm in der letzten Zeile hat $y+2$ Exponenten. Bei $x > 4$ gehen uns die mathematischen Symbole aus. Schon $Ack(4,2) = 2^{65536}-3$ hat 19728 Dezimalstellen. $Ack(4,4)$ mit ihren $4·10^{10^{19727}}$ Ziffern kann niemals ausgeschrieben werden. Primitiv ist das wirklich nicht, aber praktisch?

Falls jemand auf die Idee kommt, die Funktion (in Ganzzahlarithmetik) zu implementieren: Vorher ist der Stapelbereich (Stack) maximal zu vergrößern. Auch sollte sie nur für $x \leq 3$ und $y \leq 28$ aufgerufen werden. Vielleicht ist der Rechner nächste Woche fertig … oder abgestürzt.

Die mit Abstand schlechtesten Sortierverfahren wird stets zuerst vorgestellt, damit man noch Steigerungsmöglichkeiten hat. Hier mein Vorschlag:

Bis die Zahlen in aufsteigender Folge sortiert sind.
	durchlaufe die Permutationen der Werte eines Feldes.

void permutation_sort(int n, T a[])
{
  while (std::next_permutation(a, a + n))
    ;
}

Im ungünstigsten Fall — die Werte waren schon sortiert — werden $n!$ systematische Vertauschungen zweier Werte benötigt. Es geht sogar noch schlimmer:

Bis die Zahlen in aufsteigender Folge sortiert sind,
	vertausche zufällig gewählte Werte des Feldes. 	

void permutation_sort(int n, T a[])
{
  std::minstd_rand rng(std::time(nullptr));
  while (!std::is_sorted(a, a + n))
    std::shuffle(a, a + n, rng);
}

Hier ist nicht einmal garantiert, dass der gewünschte Fall eintritt. Je mehr Einträge das Feld besitzt, umso unwahrscheinlicher wird es, allerdings ist es auch nicht ausgeschlossen. Wegen des katastrophalen Laufzeitverhaltens werden beide "Algorithmen" meist nicht ernsthaft als Sortierverfahren bezeichnet.

Unter den "echten" Sortierverfahren ist dies das schlechteste:

  Bis alle Elemente sortiert sind (n-1 mal),
      durchlaufe die Reihe und
      hole kleinere Elemente von hinten nach vorn. 

void bubblesort(int n, T a[]) 
{
  for (int i = 1; i < n; i++)
    for (int j = n - 1; j > i; j--)
      if (a[j] < a[j-1]) std::swap(a[j], a[j-1]);
}

Die zwei verschachtelten Schleifen verraten, dass $n(n-1)/2$ Vergleiche durchgeführt werden müssen. Steht das kleinste Element ganz hinten, so muss es alle davorliegenden Plätze durchlaufen (wie eine kleine Luftblase im Wasserrohr). Allein dafür werden $n-1$ Vertauschungen vorgenommen, wie das Beispiel zeigt:

[7 	4 	2 	5 	1]
[7 	4 	2 	1 	5]
[7 	4 	1 	2 	5]
[7 	1 	4 	2 	5]
1 	[7 	4 	2 	5]
1 	[7 	2 	4 	5]
1 	2 	[7 	4 	5] 
1 	2 	4 	[7 	5]
1 	2 	4 	5 	7 	  Bubble Sort: 10 Vergleiche, 8 Vertauschungen.

Die Variante

void sysiphos_sort(int n, T a[]) 
{
  int i = 0; 
  while (i < n-1)
  {  
    if (a[i] < a[i-1]) 
    {
      std::swap(a[i], a[i-1]);
      i = 0;
    }
    else ++i;
  }	  
}

kommt mit nur einer Schleifenanweisung aus, benötigt im schlechtesten Fall dennoch genau soviele Durchläufe. Bei sortierten Werten genügt jedoch ein Durchlauf.

Dies ist vielleicht das einleuchtendste Sortierverfahren:

  Solange noch etwas zu sortieren ist,
      stelle in der verbleibenden Menge das kleinste Element an den Anfang. 

[7 	4 	2 	5 	1]
1 	[4 	2 	5 	7]
1 	2 	4 	5 	7 	  Selection Sort: 10 Vergleiche, 2 Vertauschungen.

Obwohl auch hier $n(n-1)/2$ Vergleiche durchgeführt werden müssen, wechselt jedes Element höchstens einmal seinen Platz je Durchlauf. Elemente, die schon am richtigen Ort stehen, brauchen überhaupt nicht bewegt werden. Im Mittel werden nur $O(n \log n)$ Vertauschungen durchgeführt. Selection Sort ist also stets dem Bubble-Sort-Verfahren überlegen. Wegen der Ordnung $O(n^2)$ der Vergleiche ist es aber auch nur für kleine Mengen geeignet.

void selectionsort(int n, T a[]) 
{
  for (int j, k, i = 0; i < n; i++) 
  {
    for (k = i, j = i+1; j < n; j++) if (a[j] < a[k]) k = j;
    if (i != k) std::swap(a[k], a[i]);
  }
}

Für größere Mengen empfiehlt sich das Quick-Sort-Verfahren, welches die Teile-und-herrsche-Strategie (rekursiv) anwendet:

  Bei zwei Elementen stelle die richtige Reihenfolge her (bei weniger ist gar nichts zu tun),
  sonst greife ein Element heraus und teile die Restmenge so,
      dass in einer Teilmenge nur kleinere, in der anderen nur größere Elemente sind.
  Sortiere jede der beiden Teilmengen für sich. 

void quicksort(int lo, int hi, T a[]) 
{
  if (hi - lo <= 1) 
  {
    if (hi - lo == 1) && a[hi] < a[lo]) std::swap(a[hi], a[lo]);
  } 
  else 
  {
    int i = lo - 1, j = hi + 1;
    T x = a[(lo + hi) / 2];
    for (;;) 
    {
      while (a[++i] < x);
      while (x < a[--j]);
      if (j < i) break;
      if (i != j) std::swap(a[i], a[j]);
    } 
    if (lo < j) quicksort(lo,j,a);
    if (i < hi) quicksort(i,hi,a);
  }
}

[7 	4  *2*	5 	1]
[1 	4  *2*	5 	7]
[1 *2*]	[4 *5*	7]
1 	2 	4 	5 	7 	  Quick Sort: 1 Rekursion, 2 Vertauschungen.

Anzahl der Vergleiche und der Vertauschungen sind im Mittel von der Ordnung $O(n \log n)$, schlimmstenfalls $O(n^2)$. Durch die Auswahl des mittleren Elements als Vergleichswert ist der ungünstigste Fall jedoch unwahrscheinlich. Die Anzahl der Rekursionsaufrufe ist im Mittel von der Ordnung $O(\log n)$. Im schlimmsten Fall sind $n-1$ Rekursionen notwendig. Da Quick Sort für die sehr kleinen Sortiermengen am Schluss ineffizient wird, kann dann wahlweise ein anderes Sortierverfahren (z.B. Selection Sort) aufgerufen werden.

Wählt man statt der Mitte ein zufälliges Element zum Aufteilen, wird auch der ungünstige Fall mit $O(n^2)$ Vergleichen unwahrscheinlich.

Der Wert eines Polynoms $$ p_n(x) = a_0+a_1 x+a_2 x_2+ \ldots +a_{n-1} x^{n-1}+a_n x^n $$ an der Stelle $x$, dessen Koeffizienten $a_i$ (i = 0… n) in einem Feld a mit n+1 Elementen gespeichert sind, lässt sich nach dem Horner-Schema mit nur $n$ Multiplikationen berechnen:

float polynom(float x, int n, float const a[]) 
{
  float p = a[n];
  while (n --> 0) p = p*x + a[n];
  return p;
}

Abb. 3 Nullstellensuche

Die Funktion $f(x)=-1-x^2+x^3$ hat eine Nullstelle im Intervall [1,2].

Wechselt eine stetige Funktion f im Intervall [a,b] ihr Vorzeichen, d h. $f(a)\cdot f(b) < 0$, so hat sie in diesem Bereich (mindestens) eine Nullstelle (siehe Abb. 3). Durch fortgesetztes Halbieren des Argument-Intervalls lässt sich die Nullstelle immer besser eingrenzen. Nach $m$ Schritten hat das Intervall nur noch $1/2^m$ der Ursprungsbreite: nach 10 Schritten ein Tausendstel, nach 20 ein Millionstel. Die kleine zulässige Toleranz zwischen wahrem Wert und Näherung wird gern als $\varepsilon$ (epsilon) bezeichnet:

      Bestimme die Mitte xm = (a+b)/2 des Intervalls.
      Falls f(a)*f(xm) < 0, liegt die Nullstelle in [a,xm], sonst in [xm,b].
  Setze das fort, bis ym = 0 oder |b-a| < epsilon erreicht ist. 

float bisection(float lo, float hi, float (*f)(float)) 
{
  float xm, fm, fl;
  float const epsilon = 1e-10;
 
  if (hi < lo) std::swap(hi, lo);
  fl = (*f)(lo);
 
  assert(fl * f(hi) < 0); // mindestens eine Nullstelle dazwischen
 
  do 
  {
    xm = (lo + hi) * 0.5;
    if ((fm = (*f)(xm)) == 0.0) return xm;
    if (fl * fm < 0) hi = xm; else { lo = xm; fl = fm; }
  } while (hi - lo > epsilon);
  return xm;
}

Die Implementierung weist folgende Besonderheiten auf:

• Die Funktion wird als Zeiger übergeben, damit in einem Programm Nullstellen mehrerer Funktionen berechnet werden können, die allerdings ein float-Argument übernehmen und ein float-Ergebnis liefern müssen. Die zu untersuchenden Funktionen brauchen bei der Übersetzung der Bisektionsroutine noch nicht bekannt sein!
• Je Schleifendurchlauf wird nur ein neuer Funktionswert berechnet. Das ist wichtig, falls die Berechnung sehr aufwendig ist.

Die Nullstelle $x_0 = \sqrt[3]{(29/54+1/18\sqrt{93})} + 1/(9\sqrt[3]{(29/54+1/18\sqrt{93})}) + 1/3 \approx 1.4656$ der Funktion in Abb. 3 lässt sich nun numerisch finden:

float cubic(float x)  
{
  int const degree = 3;
  static float const a[degree+1] = { -1, 0, -1, 1 }; 
  return polynom(x, degree, a);   // -1   -x^2 +x^3
}
 
float root = bisection(1, 2, cubic); // ca. 1.4656 

Die Nullstellensuche lässt sich auch zur Lösung nichtlinearer Gleichungen einsetzen. Beispiel: Die goniometrische Gleichung $x = \cos (x)$ lässt sich durch algebraische Umformungen nicht lösen. Sie muss jedoch im Intervall $[0, \pi/2]$ genau eine Lösung haben, da $\cos (x)$ von 1 auf 0 monoton fällt, $x$ aber von 0 auf $\pi/2$ monoton ansteigt. Am Schnittpunkt beider Kurven muss die Differenz der Funktionswerte $\cos(x) - x$ verschwinden:

float diff(float x) { return std::cos(x)-x; }
 
float solution = bisection(0, M_PI_2, diff); // ca. 0.73909 

Mit einer exakten Vorschrift lassen sich chaotische Zahlenfolgen erzeugen. Wird zweimal mit dem selben Wert begonnen, kommen dieselben Folgen zustande. Weicht der Anfangswert jedoch nur um ein Winziges ab, kommt etwas völlig anderes heraus. Zufallsgeneratoren nutzen das aus:

  Starte mit einer beliebigen Zahl I_0 (z. B. der Uhrzeit im Computer)
  Dann berechne fortlaufend die Zahlen I_(n+1) = (a·I_n+c) mod m. 

Bei $m = 2^{32}$ erfolgt die Restbildung durch Arithmetiküberlauf. Ein minimaler Zufallsgenerator könnte so aussehen [Smith]:

#include <ctime>
 
unsigned long rand(void) 
{
  static unsigned long seed = std::time(0);
  return seed = 22695577 * seed + 1;
}

Da immer gerade und ungerade Zahlen wechseln, sollten Zufallszahlen von 1 bis 6 mit

j = 1 + (int)6.0*rand()/(ULONG_MAX + 1.0);

gebildet werden und niemals so:

j = 1 + rand() % 6;

Wie zufällig die entstehende Folge ist, hängt von a, c und m ab. Nach spätestens m Zahlen wiederholt sich die Folge. Zufallsfolgen maximaler Periode enthalten jede Zahl zwischen 0 und m (sind gleichmäßig). Bei ungünstigen Werten kann die Periode viel kleiner als m werden. Kleine Änderungen an der Funktion rand() können die Zufälligkeit zerstören [NumRecipes]:

For example, one popular 32-bit PC-compatible compiler provides a long generator that uses the above congruence, but swaps the high-order and low-order 16 bits of the returned value. Somebody probably thought that this extra flourish added randomness; in fact it ruins the generator.

1. R. Sedgewick: Algorithmen. Addison-Wesley, Bonn 1992.
2. D. Herrmann: Algorithmen Arbeitsbuch. Addison-Wesley, Bonn 1992.
3. W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery: Numerical Recipes in C: The Art of Scientific Programming. 2nd Edn. Cambridge University Press, Cambridge (Mass.) 1992.
4. J.T. Smith: C++ for Scientists and Engineers. McGraw-Hill, New York.

Lehrmaterial zum Sonderkurs "Einführung in C++" 1997/1998 am Schülerrechenzentrum Dresden. Mai 2000, überarbeitet Aug. 2002, Mai 2005, Dez. 2007, Juli 2014.