beta()

#include <cmath>

 double beta(double x, double y)  // C++17

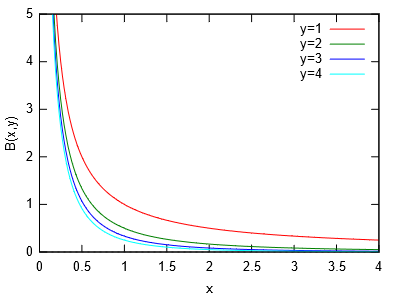Liefert Wert der Eulerschen Betafunktion $B(x,y) = \int_0^1 t^{x-1} (1-t)^{y-1} dt = \Gamma(x)\cdot\Gamma(y)/\Gamma(x+y)$.

Rückgabewert: $\Gamma(x)\cdot\Gamma(y)/\Gamma(x+y)$.

tgamma().

beta.cpp

#include <cmath>
#include <iostream>
 
int main()
{
  for (int i = 1; i <= 400; ++i)
  {
    double x = 0.01*i;
    std::cout << x 
      << '\t' << std::beta(x, 1) 
      << '\t' << std::beta(x, 2) 
      << '\t' << std::beta(x, 3) 
      << '\t' << std::beta(x, 4) 
      << '\n';
  }
}